Today kottke.org listed a chart from the Minnesota Dental Association of candies that are acidic enough to cause loss of tooth enamel. On the pH sale, where 7 is neutral and 1 is battery acid, anything rated 4 or lower will deteriorate your tooth enamel.
I'm not surprised to see my old favorite, Sweetarts, listed as a 3, and I'm sure the candies listed with lower numbers (the lowest one is 1.6!) are even more sour. My gums (and teeth) quiver at the very thought.
But in reading about the evils of acidic candies, I realized I had completely forgotten my high school science teacher's efforts. pH is logarithmic, so a 3 is 10 times more acidic than a 4; a 2 is 100 times more acidic. As with all my posts tagged Facts I Never Knew, I'm revealing my lack of knowledge, or memory, or attention from some point earlier in my life. I'm sure I learned that fact, but later it slipped out of my head.
Logarithmic scales are used to describe or display information that has a huge range of variation, so much so that if it were displayed arithmetically, there would be no detail visible on the low end. In Steven Pinker's book The Better Angels of Our Nature (lots more info coming on that book here very soon!), he uses logarithmic scales for the graphs showing the decline of violence over the centuries. If he didn't, the recent years would appear to be just about zero.
Some of the best known logarithmic scales:
- sound (bels and decibels)
- f-stops in photographic exposures
- the brightness of stars
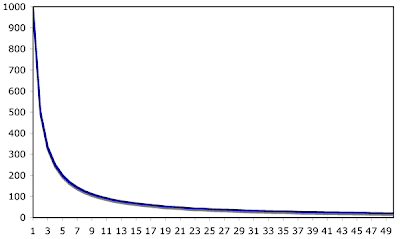
On an arithmetic scale like the one above, there's not much visual difference between the numbers at the right.
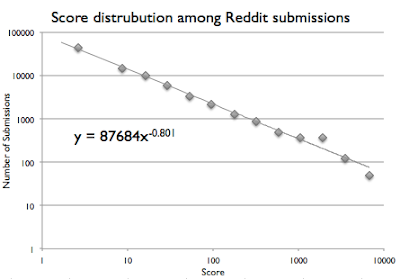
In contrast, a logarithmic scale (note the numbers along the left side go from 1 to 10 to 100, 1,000, etc.), shows plenty of detail on the right side, even though that section of the graph is describing tiny numbers like 100, compared to the top left, which is in the tens of thousands.
Very useful!
But I admit I have to keep reminding myself about the type of scale this is, since my doofy brain wants to assume all graphs are arithmetic. Which fools me momentarily into thinking the power law distribution is a gradual decline instead of the huge drop-off that it is.



2 comments:
Two more logarithmic things:
Our vision. We perceive distance between near objects while distant objects compress.
Our original concept of scale is logarithmic. When children are first introduced to numbers they'll draw large gaps between 1 and 2, which compress as they reach 10. Over time, those gaps become uniform.
This from a book I just read, "Here's Looking at Euclid" by Alex Bellos.
I read something about your second point on the Wikipedia entry. I think it also said that contemporary hunter-gatherers (preliterate) also more naturally inclined toward logarithmic scales. Fascinating.
Post a Comment